One of the strongest pieces of evidence for evolution is the ‘perfectly nested clade’. This means, when we build a hypothetical evolutionary tree for a dataset of organisms, the organisms more closely match other organisms on their branch of the tree than elsewhere.
The question is, do we see this on real world data? When we have a collection of DNA sequences from different organisms, and try to build a tree, does the tree exhibit this ‘perfectly nested clade’ property? How do we measure such a match?
The measurement of how well the dataset matches the tree is called the phylogenetic signal.
One of the most popular metrics for measuring phylogenetic signal is called the consistency index.
It is very popular partly because of its simplicity. Say we have a dataset of 3 organisms, each organism having 4 genes, and the genes are drawn from a pool of 8 unique genes. We start by counting the total number of unique genes in our dataset, which is 8. We call this number R.
Next, we look at the ancestors of our tree. Let’s say the tree has 2 ancestors. Each ancestor has its own collection of genes. For each node in our tree, whether leaf or ancestor, we subtract from its genes all the genes in its ancestry, leaving only the genes that have never appeared before in the node’s evolutionary history. This subtraction process leaves us with a collection of delta scores, which we then sum together to get the tree length, denoted by L.
Our consistency index is simply c = R/L. The intuition behind the index is that if genes emerge only along a path through the tree, and don’t pop up randomly along other paths, then c will be close to 1. On the other hand, if genes are popping up willy nilly in the tree, then c will be close to 0.
However, c only gets us half way to the phylogenetic signal. We also need an idea what c values to expect under the willy nilly (random) scenario. When we have a good idea of what a randm c value looks like, then we can place a statistical bound on c value that we can say are non random. When c passes this non-random threshold, at that point we say the dataset possesses phylogenetic signal.
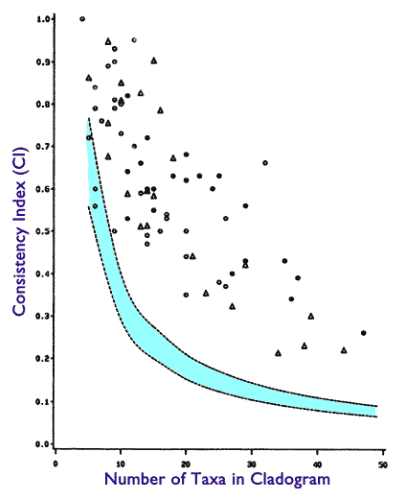
The much lauded example of using the consistency index to measure phylogenetic signal objectively is the Klassen 1991 paper, which has a nice graph pasted below. This paper is held up by the Talk Origins website as very rigorously establishing that species follow the ‘nested clade’ structure much, much better than expected due to randomness. You can see the writeup here.
Seventy-five independent studies from different researchers, on different organisms and genes, with high values of CI (P < 0.01) is an incredible confirmation with an astronomical degree of combined statistical significance (P << 10-300, Bailey and Gribskov 1998; Fisher 1990). If the reverse were true—if studies such as this gave statistically significant values of CI (i.e. cladistic hierarchical structure) which were lower than that expected from random data—common descent would have been firmly falsified.
And here is the plot of the CI index of the 75 different studies compared to the random CI cutoff. As you can see, most of the studies are well above the random CI cutoff, which according to the theory means all these datasets follow the ‘perfectly nested clade’.
Can we infer evolution from such great statistical significance? Note, the write up claims the converse would falsify evolution, which is indeed true. However, all this statistical significance does not itself verify evolution. Let’s look at the implication being argued:
- common descent → nested clades
And let’s look at what we observe:
- nested clades
However, we cannot go from 1 and 2 to prove common descent, as this is the fallacy of affirming the consequent. All we can hope to prove with nested clades is apply modus tollens:
- not nested clades → not common descent
Thus, nested clades is not evidence of common descent, nor evolution.
As a quick and simple counter example, let’s see a situation where a perfect CI score of 1 is compatible with zero phylogenetic structure (i.e. no tree).
Here we have 3 organisms with 5 genes each (letters are genes):
- ABCDE
- FGHIJK
- LMNOP
Let’s calculate R. Since there are 3 organisms with 5 genes each, then R=3*5=15.
Alright, can we build a tree for this dataset? None of the organisms have any genes in common, so the only tree we can build is a star, where all the organisms have a single ancestor, and this ancestor has zero genes.
What is the length L of the star? Since the delta scores are precisely the gene counts for each organism, then L=3*5=15.
Now, let’s calculate the c value for our scenario. Since c=R/L, then in this case c=15/15=1.0. A perfect consistency index score!
Additionally, even for such a small number of taxa the c score of 1.0 is well above the random cutoff threshold. Or, if it were not, then we can easily extend our scenario to have whatever arbitrary number of taxa required, each with its own unique set of genes, and the score will continue to be 1.0, well above the random cutoff threshold.
So, here we have a scenario that can be repeated to any desired level of statistical significance, which achieves a perfect c score with absolutely no phylogenetic structure!
This is why we cannot invert the implication:
common descent → nested clades
to be:
nested clades → common descent
since it is trivial to come up with a counter example where this is not the case.
It is also easy to come up with more sophisticated counter examples, such as directed acyclic graphs or randomly generated taxa, but this serves to illustrate the point: ‘perfectly nested clades’ is not evidence for common descent, especially not as presented in the Talk Origins article.
If you want to see more complex scenarios that also easily exceed the random CI cutoff, as well as exceeding all the values in the plot, without evolution, see the source code simulation here. You can run it in your browser and reproduce my results!
https://repl.it/talk/share/The-Phylogenetic-Signal-Fallacy/52293
You can see pictoral examples of the more complex scenarios created by the simulation here: Fallacy of the Phylogenetic Signal? Part 2 - #148 by EricMH