I’ve made the argument a couple times on this forum that phylogenetic signal does not tell us whether evolution occurred, since non evolutionary theories will also exhibit a phylogenetic signal. Since the phylogenetic signal cannot discriminate between competing theories, it is not support for evolution.
This is part 1 of my demonstration going over the approach. Part 2 can be found here:
I have written a script to demonstrate this fallacy. The basic idea is it generates datasets a couple different ways, one in line with evolution, and two non evolutionary ways. I then measure the phylogenetic signal in each dataset, and show the non evolutionary datasets actually exhibit stronger phylogenetic signal than the evolutionary dataset.
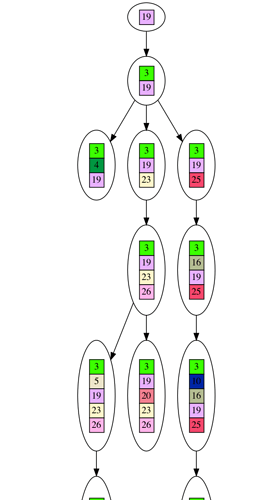
As a demonstration, here is a dataset generated from an evolutionary tree. The dataset is the leaves of the tree, and I’ve shown the entire tree. It’s a bit long, but this way you can see everything on your screen without scrolling sideways.
It is a very simplistic form of evolution, where each node in the tree represents the generation of a new gene, and no genes are ever lost. If you look closely at the graph, each node in the tree contains little colored boxes with numbers. You can think of each colored box as representing a gene. If two boxes share the same color/number they are the same gene. You can track how the genes accumulate as you trace down the growing tree to the leaves.
Each leaf in the tree you can think of representing a current day species, with its collection of genes picked up during the course of evolution. We cannot time travel backwards to look at the previous nodes in the tree, so we will need to infer these nodes. I will give an example of this inference after the tree picture below (you’ll need to click on the picture to see the full tree, and will need to download it to be able to zoom in on detail).
Alright, so now you’ve seen what is meant by evolving a tree with this script, and the kind of dataset it generates. If you look at the leaves of the tree, for instance the leaf with the numbers: “3, 5, 8, 13, 14, 18, 19, 21, 22, 23, 24, 26” is part of the dataset, but the parent node is not part of the dataset. Also, the leaf with the numbers “3, 4, 19” is part of the dataset. Altogether, there are 10 leaves in the dataset.
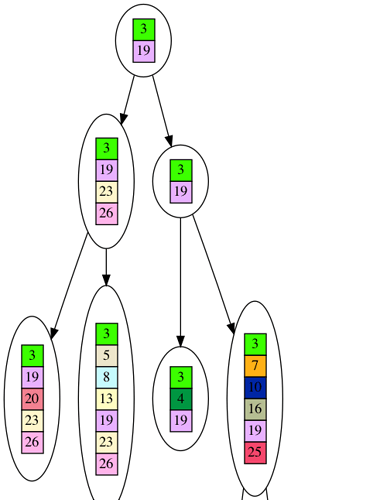
Now that we have the 10 leaf dataset, the question is how do we infer the tree? We cannot travel backwards in time to look at the older nodes, so we have to guess what the ancestors looked like. We will keep the simplistic assumption that genes are never lost, and try to determine what the tree will look like if genes constantly accumulated and were never lost. Here is an example of such a tree inferred froum our 10 leaf dataset (you need to click on the picture to see the full tree, and will need to download it to be able to zoom in on detail).
You’ll notice the tree is much shorter. This is because in the inferred tree nodes are only introduced for speciation events, i.e. branches in the tree. But in the actual evolutionary tree nodes are introduced whenever a new gene appears. If you imagine in your mind squishing the lines of single nodes in the evolutionary tree, you can see how you end up with the inferred tree. Thus, the inferred tree is a faithful, although compressed, reproduction of the evolutionary tree. It looks like our tree inference algorithm is dependable.
But, we cannot rest easy yet. There is a chance, although small, that the observed dataset of 10 leaves was generated by chance of giant leaps instead of through incremental evolution. This is our null hypothesis. To infer a tree, we want to reject the null hypothesis. How do we form and then reject this null hypothesis?
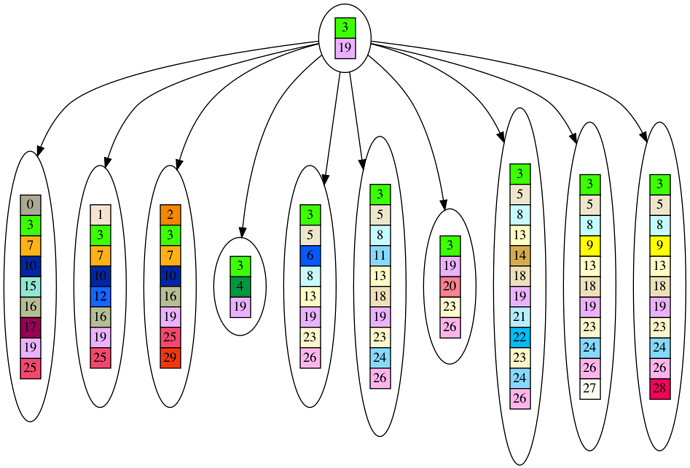
The null hypothesis is that our observed dataset was generated by a star shaped graph instead of a tree. You can see the null hypothesis next. You’ll note there is only one parent node, which contains the few genes common across our 10 leaf dataset.
Finally, our question is, how can we quantitatively reject the null hypothesis in favor of our tree hypothesis? Intutively, if our dataset contained a large number of genes in common, it is not a very big leap from the common pool of genes to each leaf. In which case, we cannot reject the null hypothesis in favor of the tree. We can think of this null hypothesis as a sort of creationist scenario, where a common kind forms the basis of evolution for all the species we see today. I.e. on the ark there was a hippopotamus/horse/cow predecessor, which quickly mutated into the diverse species we see today.
On the other hand, if there are few genes in common across the dataset, then the common kind hypothesis is highly improbable, and our dataset is more likely represented by a large number of small mutations.
To quantify the probability of these two scenarios, we take the gene delta between the parent and child node. For example, if the parent is “1, 2, 3” and the child is “1, 2, 3, 4, 5”, the delta is “4, 5”. The delta is two genes. We then exponentiate 2 to the power of this gene count. In this case, it is 2^2=4. For the entire graph, we sum all the exponentiated deltas to end up with a final score. This score represents the probability inversely, i.e. a very large score indicates a very small probability. Thus, the graph, either tree or star, with the smallest exponentiated delta score is the winning hypothesis. In the case of our example, the tree hypothesis turns out to be the winner.
So, hopefully this explanation clarifies how we infer a tree for a dataset, and how we measure whether the tree is a better fit for the dataset than the null hypothesis, i.e. the phylogenetic signal of the dataset.
Next installment we will measure the phylogenetic signal for datasets generated in a non evolutionary manner.