In my last installment, I explained how to test the phylogenetic signal in a made up dataset, in an admittedly simplistic manner.
The phylogenetic signal is a statistical test to determine whether a proposed evolutionary tree is a good fit for the data. The basic idea is, can we build a tree from the data where the traits seem to follow the tree structure, vs just pop up randomly in various locations in the tree.
Why does all that matter? It has been said on this forum and elsewhere that one of the best evidences for evolution is how the genetic data forms ‘perfectly nested clades’, or in less technical terms, the genetic data forms a tree where the genes only travel down branches and not sideways to other branches. This is what we would expect if species evolved. If we were able to retrieve the genetic record looking backwards in time, we would expect to see genes to be passed on from ancestor to children in an unbroken chain, whereas genes would not be passed from one lineage to another independent lineage. Since we cannot travel back in time to do this, and can only work with present species, we should expect to be able to derive a tree from the genetic data that exhibits this unbroken chain of gene passing without lateral transfer.
Now, things are not quite that simple. There is evidence of lateral gene transfer, and there is also the issue that genes can disappear from a lineage. These two factors alone mean we do not expect a perfect tree. There will be some measure of deviation. But still, we should expect at least a ‘pretty good nested clade’, whereby the derived tree should still be statistically distinguishable from a tree with randomly distributed genes, and there should be only one way to create an optimal tree from the data, or at least we shouldn’t be able to create a number of dramatically different trees that have the same goodness of fit to our dataset. There are other issues, too, such as the creation of an optimal tree is a very difficult problem, and cannot be done except on very small datasets. We will ignore all that for now, and just focus on the building of the trees from the dataset, and measuring whether they are pretty good, and making sure we can’t build significantly different, but equally good, trees.
My contention is that these criteria, that we can build trees with non random genes, and we cannot build divergent trees, is not uinque to datasets that are generated by evolution. On the contrary, we can have datasets generated according to other models which can achieve equal, or perhaps even better, fit for these criteria than datasets created by evolution. In other words, we can generate non-evolutionary datasets from which we can derive a tree, which exhibits a strongly non-random character.
Last section introduced my basic methodology. The methodology is indeed basic, and does not really encompass my goal above. This is partly because I don’t understand the phylogenetic signal methodology used by scientists well enough to reproduce it myself, and also I want to start with a fairly easy to understand model so myself and interlocutors can all be on the same page. Thus, what I am about to show is quite limited, and does not conclusively substantiate my conjecture. Nevertheless, it does illustrate the path I am taking, and allow others to follow along. So, let us proceed.
Last time around I created a dataset through a simple evolution model, which constructs a tree graph, and then adds a new gene for each node in a lineage. Genes are never lost. I then take the leaves of the tree, and use a simple clustering algorithm, derive a tree from the dataset. I then compare the tree to a star model. The star model takes the genes common across all the leaves as the origin node, and the leaves are the spokes. The tree and star are compared for the dataset using a metric called sum of delta scores (SDS). The basic idea about the SDS is to score how much divergence there is between the genes of parent and child, across all the edges in the tree. A large score indicates there is a large divergence, and a small score a small divergence. A smaller score thus indicates a more concise description of the data. There are some concerns about whether this is a sufficient statistic, but it does at least capture some aspect of genes following a lineage, albeit not perfectly. The key point regarding SDS is that comparing two models for a given set of leaves, the model that describes the data more concisely will receive a lower SDS score. If the leaves can be decomposed into a tree structure, then the tree structure will have a lower SDS score than the SDS score for the leaves by themselves.
This time around, I will introduce two new models. The first model is the directed acyclic graph (DAG), and the second model is randomly generated equal length leaves. Both methods of generating datasets result in datasets that fit the tree much better than the star, and do this better than the dataset generated by evolution. As for why this happens, it will become obvious as we look at the graph visualizations. The reason is the star can only fit the dataset better than the tree when all the leaves have genes in common, and this condition will almost never happen with the DAG and random methods of generating leaves, but will always happen when leaves come from an evolutionary generation.
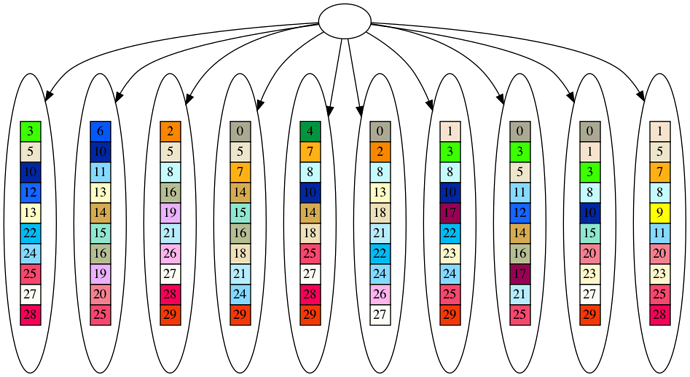
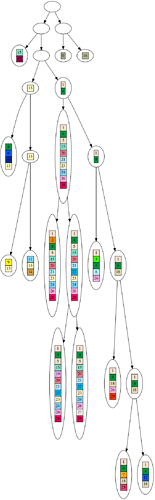
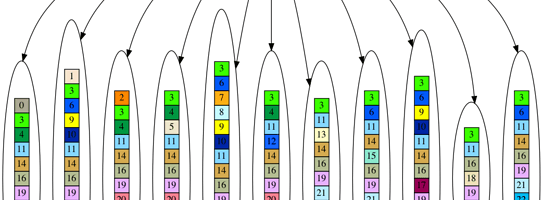
Now, enough with all the buildup, let’s see these alternate methods. First, we will look at the randomly generate leaves. The star graph for the leaves and the leaves themselves are the same, since randomly generated leaves almost never all share a collection of genes in common. As in the last installment, the genes are colored boxes with numbers, and two boxes of the same color and number are the same gene.
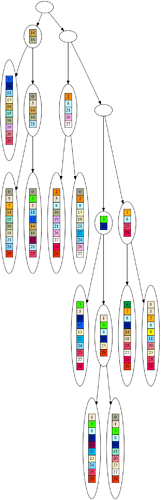
Now for the tree that is derived from this dataset. Since two leaves can share some of the same genes in the dataset, it is almost always possible to derive at least a partial tree from the dataset. I say partial, because you will see the nodes closer to the root tend to be empty, as we will reach incompatible nodes that do not share any genes. However, in a tree, all nodes except the root must have a parent, so even incompatible nodes will have a parent, which will necessarily be empty.
You will need to click on the graphic to see the full tree, and you will need to download the graphic to see all the detail. Again, this in the tree derived from the same dataset displayed above.
So, that is the randomly generated dataset and star and tree derived therefrom. As we discussed regarding the SDS metric, if a dataset can be decomposed into a tree at all, it will always score better (lower) than the dataset itself. Since the random dataset never shares common genes, the star root will always be empty, and the star model will always be equivalent to the dataset itself. On the other hand, there will always be leaves that share genes in the random dataset, and so the dataset will always be decomposable into a partial tree. This means that the randomly generated dataset will always fit a tree much better than a star according to the SDS metric. On the other hand, the evolved dataset must always share at least one gene amongst the leaves, if not more, so there is always the possibility the evolved dataset can fit a star model better than a tree according to the SDS metric. As a consequence, the randomly generated dataset has a better phylogenetic signal (at least in this formulation of the phylogenetic signal) than the evolved dataset.
Finally, let’s look at a DAG generated dataset. In this case, we will look at three different graphs. The first graph will be the actual DAG that created the dataset. The second graph will be the star derived from the DAG dataset. The final graph will be the tree derived from the DAG dataset. We will see the same situation applies, where a DAG dataset will almost never share common genes, and thus will always fit a tree better than a star, and consequently has a better phylogenetic signal than the evolved dataset.
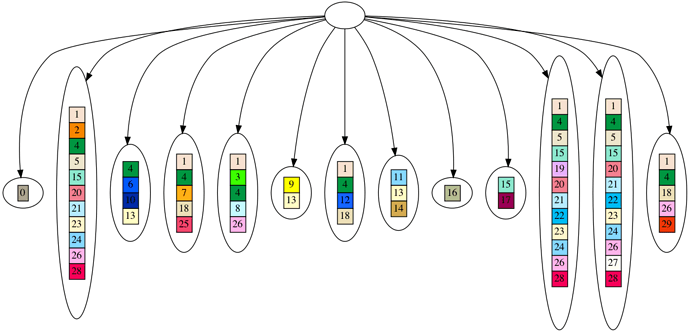
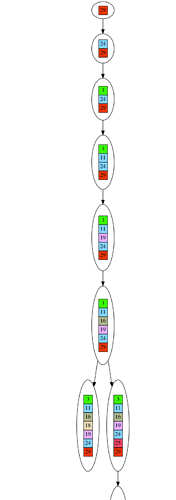
Now, here is the original DAG for the dataset we will be examining. Before looking at the star, think about the characteristics of the DAG, and whether we expect the star to ever have genes in the root, i.e. whether the leaves will ever share a common set of genes.
Click to view the full graph, and download to see the full detail.
Next is the star for the same dataset. Note the reason why a DAG is unlikely to produce a star with a filled in root. It is because the DAG can have multiple roots, and if there is ever more than one disconnected root, there will always be two leaves that do not share any genes. Since the DAG is randomly generated, and for the parameters chosen, there are more DAGs with multiple disconnected roots instead of one root, then DAG datasets will almost always generate stars with empty roots.
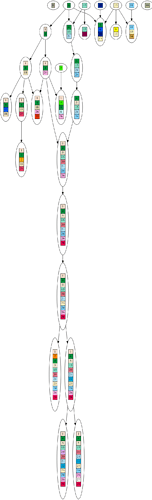
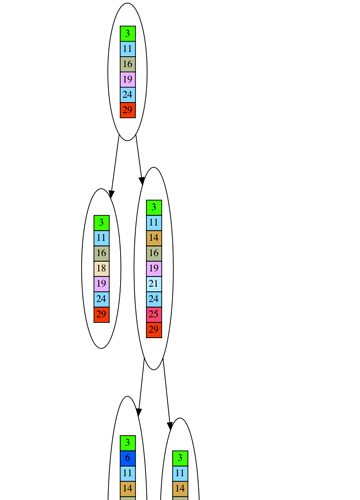
Finally, let’s look at the tree graph for the DAG dataset.
Click to see the full tree. Download to see the full detail.
Since the DAG is likely to contain subgraphs that have some element of tree structure, thus it is likely there will be at least two leaves that share genes, and thus it is likely the DAG dataset can be decomposed into a partial tree. As discussed, any dataset that can decompose into a partial tree will receive a better SDS score than the dataset itself. Therefore, the DAG dataset is going to have a better phylogenetic signal than the evolved dataset.
This concludes the second installment of alternative models.
What can we learn from this investigation? Of course, it is a very simplistic take on the whole question of phylogenetic signal, and does not compare in the slightest to the mathematical rigor in the actual science of cladistics. This investigation serves as a thought experiment, to show there is a possible world, with some assumptions and methods that match the actual world of cladistics to some extent, in which evolved datasets actually possess a lower phylogenetic signal than non evolved datasets. So, in this possible world, the fact a dataset exhibits a phylogenetic signal is not evidence the dataset evolved. On the contrary, exhibiting a strong phylogenetic signal actually indicates the dataset did not evolve.
What does this investigation say about the real world of cladistic science? It of course does not call into question the entire enterprise. However, the investigation at least serves as a qualifier. It shows that we need to say a bit more about the dataset and its phylogenetic signal in order to infer the dataset evolved. The mere fact a dataset exhibits a phylogenetic signal according to some definition does not in itself indicate the dataset was generated by evolution.