I am sorry. I don’t understand.
What would you say are black holes? Thanks.
Of course, not true, as while in general the universe is expanding, locally, stars and galaxies may move toward one another, collide, merge and so forth, and within galaxies, neighbor stars stay pretty much in the same general neighborhood. The stars in the constellations described in Job are pretty close to the same relative positions.
Wikipedia has a nice article on star formation, though am sure much is yet to be learned. I am sure we both believe God made the stars, but curious as to what mechanism you believe was used, since that gets us down to that level. And is it compatible with astronomical observations?
1 Like
Do you see any place in Boyle’s law for including the effects of gravity? That is something you have to allow for when you are talking about a cosmic scale.
This does not become more true with repetition. You seem to be under the mistaken notion that there is some conflict between Boyle’s law and gravitational collapse. There is not. Boyle’s law, as are all formulations of gas laws, are fully incorporated into the virial equations and Jeans instability for GMC [Giant Molecular Cloud] collapse and star formation. Chapter 6 of the link I provided addresses the balance of thermal energy against gravitational attraction and the math is fully developed - there is no contest here.
Since every GMC we have seen is larger than this size, and there are clearly always perturbations present, this means that molecular clouds cannot be stabilized by gas pressure against collapse. Of course one could have guessed this result just by evaluating terms in the virial theorem: the gas pressure term is very small compared to the gravitational one. Ultimately, the virial theorem and the Jeans instability analysis are just two different ways of extracting the same information from the equations of motion.
Notes on Star Formation
For any interested, the following is a nice You Tube video discussing some interesting observations of star formation in process:
2 Likes
Look, Patrick, you need to start doing some very basic maths here.
You’re taking the way that gases behave on laboratory scale and assuming that they behave in exactly the same way on a galactic scale. They don’t.
The strength of the gravitational field due to a gas cloud at its edge is given by the inverse square law:
g = \frac {GM} {r^2} \hspace 2em [1]
For a given density, the mass is proportional to the volume, in other words, to the radius cubed. For a spherical gas cloud:
M = \frac 4 3 \pi r^3 \rho \hspace 2em [2]
Putting [2] into [1] gives:
g = \frac {4 \pi G r^3 \rho} {3 r^2} = \frac {4 \pi} 3 G \rho r
In other words, for a gas cloud of a given density, the gravitational force that it exerts at its edge is proportional to its radius. Of course it will start to contract once it gets to a certain size.
Seriously, this is the basics. It’s beginner stuff. It’s the level of physics and maths that teenagers learn at school.
3 Likes
That seems to be a rather dogmatic statement.
1 Like
Ever the charitable one, aren’t you, T!
2 Likes
There are at least several verses that say he spread out the heavens like a curtain or a tent.
Psalm 104:2, Job 9:8, Isaiah 40:22
I have what if’s
What if time is relative, beginning where man was created? Here. Everything was created here (relatively) and spread out from here.
Think of it this way. Gravity is so negligible where gases are concerned, that just static electric forces will keep them apart. And back to more pressure = more activity = the gases expand.
Theoretical.
What is the sun made of and what holds it together.
Why does the earth have an atmosphere that hasn’t floated away.
What causes atmospheric pressure.
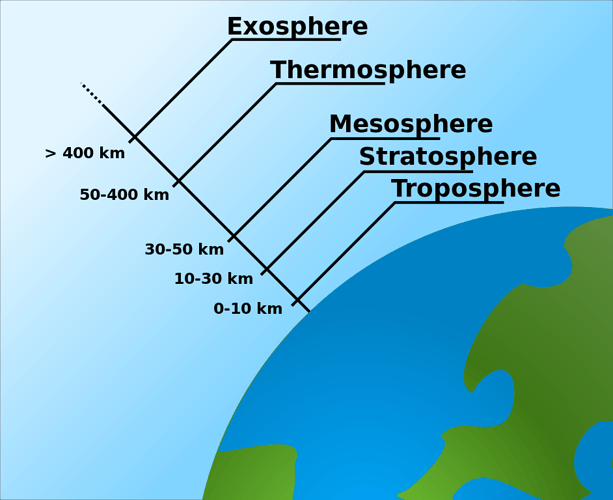
Why is air thinner at high altitudes and why do airliners have oxygen masks.
Did you even read my last post, Patrick?
I just showed you the maths that demonstrated that on an interstellar scale, that is simply not true. Gravity is not negligible.
1 Like
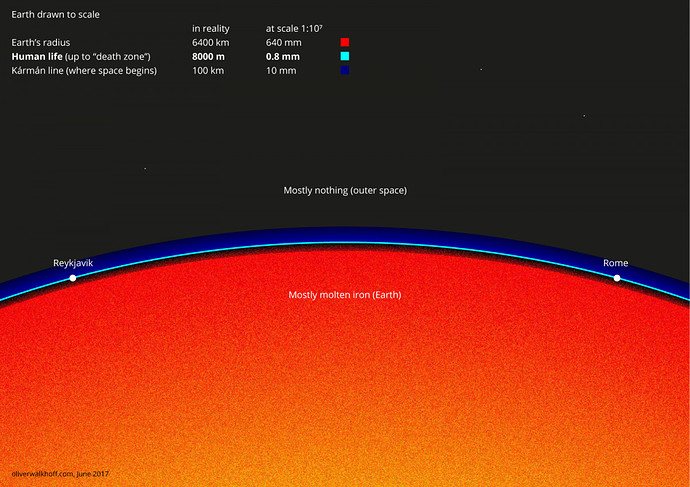
You may not want to think about this one too closely. We find pictures of the atmosphere online like the following, but they are hopelessly out of scale.
This one is to scale. And you see how far out the atmosphere extends on a planet with a mostly iron core.
Now tell me how gases alone are going to have enough gravity to form a sun or even a gas planet when the whole earth can only hold this much atmosphere.
You have not answered any of my questions and your thinking intuition is hopelessly out of scale.
How can the Sun have such a strong gravitational field if it’s made of gases? (Beginner)
Whether it’s a gas or a liquid or a solid doesn’t make any difference.
Easy. Done. Science quantifies. You have already been given the math in prior posts.
Here is yet another paper which mathematically demonstrates your reasoning to be wrong.
Boyle’s law and Gravitational Instability
False. While the Hubble constant dominates for distant galaxies, that is not at all true for stars and nebula in the milky way. Andromeda galaxy is approaching us at about 110 kilometers per second, and will meet in about 4 billions years.
1 Like
Do you know of any spherical gas clouds? And how do you apply the gravitational speed at the surface of the earth to a cloud of gas? There is no down in a gas cloud. And they are not compressing.
Information:
Compared with diffuse nebulae ( see H II region), planetary nebulae are small objects, having a radius typically of 1 light-year and containing a mass of gas of about 0.3 solar mass.
Astronomers called them planetary nebulae because of their observational similarity to Uranus, but we now know they are the remnants of dead stars and have nothing to do with planets.
The duration of the planetary nebula stage for stars can be estimated quite simply in the following way:
- From spectroscopy, the expansion velocities of planetary nebulae are estimated to be approximately 20 - 30 km/sec.
- We can use the standard right triangle technique to determine the physical size of a planetary nebula if we measure its angular size and its distance.
- If you calculate size / velocity, you can estimate how long a particular planetary nebula took to expand to its current size.
- For a typical planetary nebula, its radius is of order 1 light year, or 9.5 x 1012 km. So 9.5 x 1012 km / 25 km/sec = 3.8 x 1011 seconds, which is approximately 12,000 years. The largest planetaries have ages determined in this way to be less than 50,000 years.