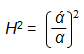R Spier's Young Universe Cosmology (take 2.5)

Faith & Science Conversation
1

@r_speir

The previous thread got shut down, and for good reason. It was likely to go in circles. I wanted to give the ideas a fair shot on these forums in a sense, despite not being anything more than perhaps mathematical possibilities. So, I tried to go through the material and made it to the end of the first page before my brain was fried:

Okay let’s begin.

The derivation of the first set of equations is odd. If the beginning is odd, then the rest of it would be hopeless.

  • Equation 1: okay, this is the Stefan Boltzmann law. Nothing too odd here.
  • Equation 2: what is this equation? What is this scale factor, τ? Initially it seems that you are saying that the surface area of our universe expands as a function of τ. What does tau mean exactly? You have defined things backwards from how τ is usually used as a characteristic time scale, because you defined such characteristic timescale already to be the planck time. If you look at your equation, what you are saying is that given an initial surface area, the surface area increases linearly depending on how many planck time units have passed. This equation is just wrong. By definition characteristic timescales do not change as a function of time.
  • Equation 3: given that equation 2 was so odd, this one is also destined to fail. However, you did do the correct substitution of the Planck length for the Planck time.
  • Equation 4: seems like a lot of work to just derive the equation that only describes the observable universe. If the speed of light has indeed remained constant, then yes, the observable universe has a radius grows at the speed of light in all directions. The surface area of such a sphere is given by exactly what you wrote: A=4piR^2=4pi(ct)^2.

All of these equations don’t really make sense in light of cosmological models for the scale factor of the universe. Why go through the trouble since it’s already pretty well established that the scale factor depends on the density of radiation vs. matter vs. dark energy. For example this graph is a very common graph in cosmology:

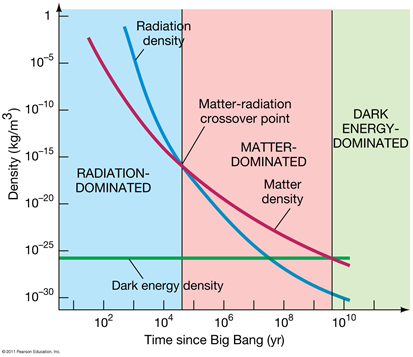
In different eras, you can derive the scale factor of the universe, like the radiation dominated era scales the radius of the universe like R~t^(1/2), the matter dominated R~t^(2/3), as outlined here: Scale factor (cosmology) - Wikipedia.

This is not going well, but I did skim the second page. You mention the so-called flatness problem that is “unsettling” with no “scientifically satisfying answer.” That’s not true at all. There are many good solutions, with the leading one being inflation which has produced a good 12,000+ papers since its inception by more than 9,000 different cosmologists. Anyone can casually read the wikipedia entry: Flatness problem - Wikipedia. I am personally pulling for cosmic inflation which we have some evidence for, but it’s not quite as nice as we’d like just yet.

I can’t do any more :ambulance:

2 Likes
2

This seems related to a blog post earlier on BioLogos.

http://biologos.org/blogs/deborah-haarsma-the-presidents-notebook/light-matters-is-einstein-a-friend-of-young-earth-creationism

3

Incorrect. Planck time is a fundamental constant - the ground floor moment of the universe - with no “passage” of anything occurring. Tau is simply a term choice to describe the passage of time associated with the growth of the thermodynamically active surface area of the sphere. Tau over lp (Planck time) is a dimensionless dynamic. Tau moves while Planck time “stays put”. When Tau / lp is multiplied by Sp, we see Sp become dynamically active. There is absolutely nothing wrong here. No rules have been broken.

Let’s camp here for a moment (though I have all your answers ready). How would you mathematically describe the growth of a sphere surface area without using the radius?

4

Look at the comments sections of these articles. I made several comments in total agreement with the author.

5

Perhaps I wasn’t describing the oddity of that equation very well. What the equation says is that the surface area of the universe is a function of ‘tau.’ Like if I were to plot the surface area of the universe that would go on the y-axis. And then the x-axis would be what you’ve called ‘tau.’ If the value at tau = 1 Planck Time is what you’ve called Sp, then when tau = 5 Planck Time the surface area would be 5 Sp. After 1 second has passed, you would say that the universe is now larger than Sp by a factor of 1.86 x 10^43. If the time at 1 second is equal to Sp2, then the surface area of the universe 13.8 billion years later would be 4.4 x 10^17 times larger than Sp2. Or the universe had half the surface area when it was half its present age. In essence, you are saying that the surface of the universe scales linearly with time. That would of course be in agreement with the radiation dominated era that is described above but your equation hasn’t described the actual expansion of the universe for 13.79999 billion years.

1 Like
6

You are really looking at this. Ok, let’s make some course corrections on your figures and you should then see what it happening.

You are off by one exponent. The correct figure should be 1.86e43. But remember that is surface area. You must divide by 4pi to arrive at linear meters squared to evaluate the scale factor. And don’t forget to multiply by an Sp value for a young universe, or .06 square meters. So 1.86e43 * .06 / 4pi = 8.88e40 meters squared.

Now, if you want today’s full expansion of the tau time zone (and it seems like you do), then you must multiply by 6000 years of seconds (not 13.8 billion years of seconds). So 8.88e40 * 1.89 e11 = 1.67e52 meters squared. Now take the square root of that figure to arrive at today’s full expansion of the tau zone, or 1.295e26 meters.

7

Thanks, I fixed by exponent and yes I know it’s referring to surface area but thanks for the reminder.

I’m sorry, but what? How do you know what the Sp value is for a young universe? What your equation says is that that surface area of the entire universe (which doesn’t necessarily make sense if the universe is flat and unbound) when the age of the universe is 1 planck second (or 5.39 x 10^-44 seconds old) is 0.06 m^2. Hmm I wonder how you chose that number? Do you or anyone actually know what size the universe should have been when it was one planck second old? Nope. But you actually chose the number such that you would arrive at the number 1.3 x 10^26 meters as the present day radius. Why did you want to arrive at that number? Because, that number is the radius of the observable universe, or 13.8 billion light years in radius.

In other words, you hand picked an initial surface area (appropriate for a ‘young universe’) such that you can easily force 6,000 years of seconds into somehow describing our actual universe.

And again, this universe that you are describing is one where the radius scales like t^(1/2). That universe is predicted by standard cosmology equations but does not describe a universe that is dominated by matter and later dark energy which is where our universe is currently at unless something changes that we don’t yet know about.

1 Like
8

But the universe is much bigger than the observable part, right? How would that impact the analysis?

9

"[quote=“pevaquark, post:7, topic:36604”]
In other words, you hand picked an initial surface area
[/quote]

Remember in the paper I told you it was a free parameter?

“just how much time has elapsed on the CMB clock from the beginning is a parameter determined solely by the size of Sp, the surface area of the primordial sphere”

Creationists could argue that the universe surface area was about .06 sq meters when it came into being at the Planck moment. And the important thing is nobody could stop them.

10

Hi r,

As I mentioned to pevaquark, cosmologists have strong reason to believe that the universe is far larger than the part that is observable from our planet. How would that affect your analysis?

Thanks,
Chris

11

Remember the paper concluded with this:

“…these thoughts represent a first approximation of a young universe cosmology.” This first approximation deals with a Hubble volume of √2 c dt radial meters (1.83e26 meters) and stops. If there is more to the system your question would likely be dealt with in an extension of this cosmology.

12

Yes, but that isn’t even science. It’s an ad hoc argument for a particular model that is useful for nothing except convincing other YEC what they already want to believe is true.

It depends on two things (and why are you talking about the CMB now?)… one, yes the size of the primordial sphere which you hand selected to allow for 6,000 year seconds to expand to the present day size of the observable universe… and it assumes that the scale factor of the universe is R(t)~t^(1/2). That is an incorrect assumption, only valid as a solution when the universe is dominated by radiation. You don’t even provide a derivation of your initial equation for the surface area, just assume that it scales linearly with time which you absolutely cannot do, ever in physics. And then of course the universe would only be dominated by radiation for approximately 0.0001% of it’s lifetime to date.

2 Likes
13

Are you sure? Because we could also find the surface area of the primordial sphere for a 13.8 billion year old universe rather than a 6000 year old one. It would be very small indeed. Would that make you happier about the science here?

You are the one who keeps camping on the CMB expansion in this model, not me. Did you forget there is also a Hubble expansion?

You are going to have to drop the topic of Friedmann’s solutions under ideal states like Rt is proportional to 1/2t in the radiation era and Rt is proportional in 2/3t in the matter dominated. In the universe we will always have a mixture of dust, radiation, and dark energy and Friedmann solved that condition simply with a’ / a. And I have already dealt with that in the paper

Look here

https://www.cfa.harvard.edu/~ejchaisson/cosmic_evolution/docs/fr_1/fr_1_part1.html

“The cosmological principle is valid even though the Universe is expanding. Like that of any static sphere, the surface of an expanding sphere has no center, edge, or boundary.”

Without a center, we cannot identify a radius. Remember we are dealing with the surface area of the supreme ideal blackbody in nature - the universe. I asked you this question before so I will ask again. Without a radius, how would mathematically describe the surface area of a thermodynamically active sphere?

14

I already know it is t^1/2 and t^2/3 so no need to make the correction.

15

Yes. I am sure. It is pseudoscience at best. Completely untestable, chosen ad hoc so your model matches some aspects of the observable universe. There are some numbers occasionally in models of the early universe and yes, they are very tiny. Perhaps a more reasonable size to start is more comparable to the planck length. I don’t really know though and we definitely can’t measure it.

I literally mentioned it zero times until you brought it up. And the CMB expansion/Hubble expansion/distinction is something you made up. Do you mean the CMB photons increasing in wavelength over the past 13.7 billion years?

Yes there is indeed a mixture of stuff always in our universe. You know the approximation is a good one to give a good sense of what the real universe actually should do. The real exponent would be somewhere in between each one depending on the particular era. It’s a clever idea and physicists do it all the time to get a good sense of what should/would be happen in extreme/limiting cases.

Not sure what you mean exactly. Actually let me clarify. I have no idea what you are even saying with this question. What is a thermodynamically active sphere? Maybe I need to start reading papers like those summarized here: Physics - Active-Matter Thermodynamics Under Pressure.

I wouldn’t be so petty as to belittle your intelligence with such remarks. But I must confess that your model seems really weird to me beginning on page 9. You have God making the heavens and the Earth and then crunching it all back together before one planck time has passed, before letting it all expand again. Or 380,000 years of real time occurs in .128 tau seconds.

No unique predictions, some failed predictions
I think that your model suffers from no unique predictions (you’ve basically described most of the standard understanding of the early universe). All your predictions are done after the original model predicted and measured several of them (like the only light elements prediction from nucleosynthesis). The production of heavier atoms did not occur in this initial moment because the distribution of them is different from the very light elements. So there’s a least one incorrect prediction of your model I suppose.

God-of-the-gaps
And then you hand wave away some of the unknowns of the standard model (like the one part in a billion or so difference between matter and antimatter) by just saying ‘easy, God did that one’ in classic god-of-the-gaps type of fashion.

Interesting Plain Reading of Genesis
I don’t get the whole God makes the heavens and the Earth and its dark (all of that takes place in less than 10^-43 seconds) and then the entire universe erupts into a giant supernova (required to produce heavy nuclei) and somehow the Earth isn’t destroyed. That’s a lot to occur that isn’t said in a plain reading of Scripture which almost begs the question, why do you take it literally if you require so much to occur like the Earth getting created, then obliterated then somehow existing again outside of this explosion? It seems like so much flexibility but then you must literally read everything else.

The end of all things
I get it. You’ve thought about this longer than any of us ever will. I doubt anybody could show you to be wrong even if you were. I at least appreciate you are generally aware of the real cosmology and don’t just dismiss it like most YEC. I certainly am not up to the task anymore (though perhaps never was). I still don’t get how much real time passes for every tau second. Like after 3,000 year seconds did half of 13.8 billion years occur. I have no idea, but back to the :ambulance: for me. I promise to read anything else you post in this thread but may not have the energy to respond.

1 Like
16

I am surprised at your response for three reasons. First, the origin of the universe itself is untestable. Next, I would know better than to try and stop you from taking a ground floor surface area A in space and scaling it simply as a function of time, yet you disallow me that scientific privilege. Last, I think I made it clear that a young universe is not the only outcome of this model.

No, I did not mean that specifically but we can go there for a moment. It is actually quite beautiful in this model. You are referring to column 4. Again, this is a first approximation model, so column 6 - Hubble time - is not constrained yet by epochs of radiation or matter or dark energy domination.

image.png699×276 12.7 KB

Ok, so we agree here.

The research you cite distances itself from ideal gases. I would stick with ideal gases in studying the universe.

God’s “heavens and earth” in the Planck epoch are in particulate form, not the fashion we see today.

I am not trying to make predictions. Many times in building cosmologies, the best you can do is to offer “post”-dictions.

Good observation. That part should be revised.

Here, I am taking my liberties and adopting a behind-the-scenes look at the motivation of God just to get the universe in motion. However, we could adopt the standard scientific method approach if you want and put blinders on and not permit ourselves to “see” behind the “wall” of Planck time. Then my tone about particle-antiparticle annihilation would start sounding more like the text book versions. (While we are on the subject, I am beginning to think that the very early matter-antimatter epoch acted as a sort of “clearing of the air” to make way for the heavens and earth we now witness. I think it imparted something vital to ubiquitous space.)

See earlier comment. Heavens and earth was particulate initially and not later “destroyed then reinstituted”.

Absolutely! A huge pet peeve of mine is how YEC models just seem to cruise past the preponderance of great cosmological science out there.

The chart above should help. Aging is concurrent. The universe is aging 6000 years all the while 13.7 billion years of accelerated aging is occurring. Thanks for looking.

17

This topic was automatically closed 6 days after the last reply. New replies are no longer allowed.