This is a companion discussion topic for the original entry at https://biologos.org/blogs/deborah-haarsma-the-presidents-notebook/light-matters-what-is-light-actually-made-of
Like last time, I’ll be available here to respond to any questions and additional thoughts you might have. Feel free to ask for extra explanations on any of the topics that we touched upon.
@Casper_Hesp Thank you for this. I’m a Liberal Arts guy who easily gets lost in the technical explanations. I definitely learned some things about the nature of light. To be sure I understand, Einstein saw 2 theoretical behaviors for light (constant speed and ASC) and decided to bet on constant speed given what he knew about the characteristics of light?
Thanks, Jim
Hi Jim, thanks for asking!
I think you got the overall idea correct. To make things a bit more complicated, there are actually many different conventions possible (besides constant speed and ASC). They are all allowed as long as the two-way speed of light is constant.
Out of all the different options, Einstein indeed chose the convention that gives a constant speed of light. The wave properties of light were the most important reason for that choice. It wasn’t really a “bet”, because Maxwell’s theory was already very well established by observations.
As an aside, another benefit of Einstein’s choice is that it makes the math much easier  .
.
Hi Casper,
In the figure of the traveling lightwave both the electric and magnetic fields can have a zero value at the same time. You state: “electric and magnetic fields have an intriguing reciprocal relationship: (1) changes in electric fields cause magnetic fields and (2) changes in magnetic fields cause electric fields.” Hence the one field should be maximum where the other changes the fastest, that is where in the other the zero value is crossed. The one field should be zero where the other changes the least, that is at the other’s maximum value.
Then a smooth exchange between electric and magnetic field energy is possible where the total energy remains constant, just like a pendulum where periodically kinetic and potential energy is exchanged in a smooth way. I cannot think of a reason why most graphical renderings of electromagnetic waves are similar with yours, in any case I am not the only one who thinks that it is not correct.
See the next link.
http://www.play-hookey.com/optics/basic_concepts/transverse_electromagnetic_wave.html
Hi, Bert. I should know the answer to this question since I have an electrical engineering degree (1992), but since I haven’t used differential equations or partial derivatives as applied to Maxwell’s equations for about that long, I’ve lost the necessary math.
However, being intrigued with your challenge, I checked my physics text and sure enough, it shows the two waves in phase, and furthermore clarifies in the text that this is accurately shown as such. (So it isn’t a matter of careless illustrators accidentally misrepresenting something). What you say makes sense on the surface in an LC world where we are used to purely capacitive and inductive effects putting voltage and current 90 degrees out of phase from each other. But that property is apparently not accurately applied to the world of EM waves according to participants at physicsforums.com here over this very issue.
I can’t follow their math well enough to understand much less explain how your objection is fully answered over an apparent energy loss where both zero-crossings converge (though I remind you that a zero-crossing does not necessarily represent a zero energy state for all parameters). But maybe you can follow the site for yourself and see if the answers given are satisfactory.
Rest assured, the knowledgeable physicists that be have spoken on this, and the illustrations given as they are, are not haphazard accidents.
Hi Mervin,
Thanks for your response.
I got my degree in electrical and computer engineering in 1968 and, like you, I don’t master the math anymore.
The reference you gave me does not help me to clear things up. For me a photon is a simple harmonic oscillator with a constant energy and the graphic representation seem to suggest otherwise.
Maybe the deeper reason is that a realistic graphical representation of a propagating electromagnetic wave is not possible and that the one that is normally presented is a reasonable compromise.
The underlying math is what is important, not the picture. I was only curious.
Well, we are curious together, then, if there is something to this objection. Maybe Casper can illuminate, so to speak, in layman enough terms so that we don’t have to call on our rusty math. It is precisely because I’m not in a position to critique what is already considered well-settled that I tend to trust the textbooks on this. [But I do know that textbooks have been wrong before --so I respect that one can’t always safely do this.]
@bertmorrien @Mervin_Bitikofer
Hi Bert and Merv!
Your confusion is understandable, because of my phrasing:
“electric and magnetic fields have an intriguing reciprocal relationship: (1) changes in electric fields cause magnetic fields and (2) changes in magnetic fields cause electric fields.”
Mathematically speaking, it would have been more correct to state it as follows:
“electric and magnetic fields have an intriguing reciprocal relationship: (1) changes in electric fields cause [changes in] magnetic fields and (2) changes in magnetic fields cause [changes in] electric fields.”
This can also be seen from Maxwell’s equations, the third and fourth here:
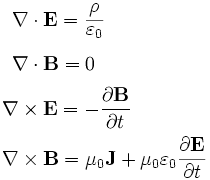
Note that the first-order derivative in space of the electric field (third equation, left-hand side) depends on the first-order derivative in time of the magnetic field (right-hand side). So if you take the first derivative of the electric field in my animation, you will see it corresponds with the magnitude of change in the magnetic field. The same holds vice versa (fourth equation).
I hope this clarified things for you. I chose for my first formulation to decrease the probability of less mathematically-minded people zoning out and losing track (changes causing changes? ![]() ). Nonetheless, it’s good that you picked this up. Thanks for reading along and asking for clarification!
). Nonetheless, it’s good that you picked this up. Thanks for reading along and asking for clarification!
HI Casper,
Thanks for your explanation. As far as I understand it, a photon is an harmonic oscillator where
electric and magnetic field energy are periodically exchanged in a smooth way. I still do not understand where the energy is when both fields are zero. But never mind, I don’t think this is the place where I should look for the solution of my problem.
Best,
Bert
Hi Bert,
Actually, your intuition is pointing in the right direction. The energy flux of an electromagnetic wave is obtained by multiplying the magnitude of the electric field with that of the magnetic field (for more reading, see the Wikipedia page on the Poynting vector). So at the points were both E = 0 and B = 0, the energy flux is zero. To obtain the total energy transported by an electromagnetic wave, we need to take the average across the whole wave packet.
As an aside, your view of a photon as a harmonic oscillator corresponds with the classical description of light. But in the quantum description, a photon is not seen as a perfect oscillator but rather as a particle or a “wave packet”. We look at what is transported by the packet “as a whole”, not at individual points in the electromagnetic field.
I hope I have managed to address your question with this.
Blessings,
Casper
Casper Hesp,
After viewing “Maxwell’s Equations and Electromagnetic Waves” via next link
I must agree that the phase difference between the electric and magnetic field strengths is zero. In hindsight It should have been clear to me that this phase difference is like the load factor (cos φ) at AC power transfer. After all, electromagnetic radiation is a form of power transfer. With a phase difference of 90 degrees no power is transfered.
Thanks again for your reactions.
This topic was automatically closed 6 days after the last reply. New replies are no longer allowed.