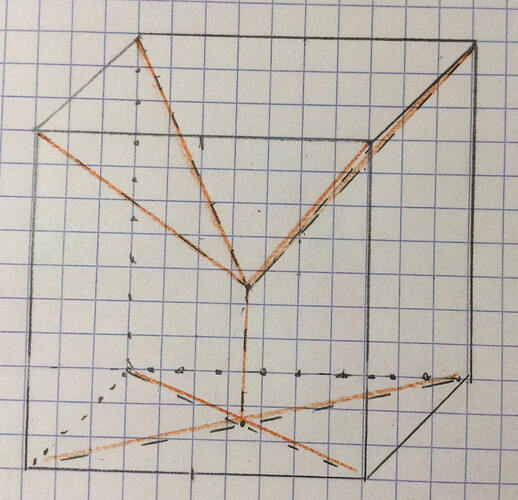- Recently, I was reminded of two different math facts.
-
Each of the three inner angles of an equilateral triangle on a plane is 60 degrees,
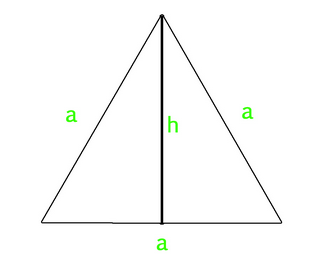
-
Each of the three inner angles of an equilateral triangle on a sphere is 120 degrees.
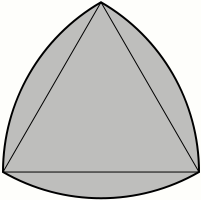
- This triangle is known as a Reuleaux triangle
-
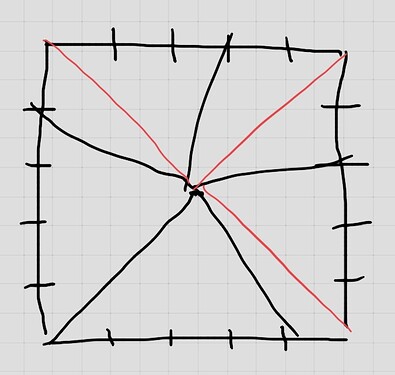
- To “see” the difference between the two triangles, compare the two triangles in this diagram:
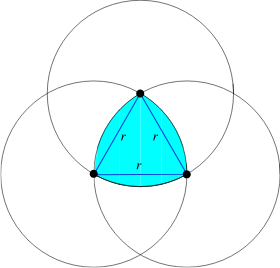
- The distance between the dots in the first triangle is shorter than the distance between the same two dots in the second triangle.
- What that tells me is that given three locations on the earth’s surface, I should expect the distances between any two locations to be smaller if the earth’s surface is flat than the distances between the same three locations if the earth’s surface is spherical, no?
- My big question is: "Have the different distances between two or more locations ever been used to prove whether the flat earth theory is more accurate or less accurate than the spherical earth theory?
Unless I’m missing something, I would say “Yes, by airlines using geodesic flight paths every day”
It’s also called great-circle navigation. (Ships in the Navy use it, Terry. ; - )
I served 3 yrs 9 mo. in the Navy. Shore duty the whole time; a couple of hours on an aircraft carrier when it pulled into Piraeus port, south of Athens, … visited a buddy stationed on it. Great circle navigation was not taught in boot camp. Algebra was not my thing until I was in my 30s and I finally had teachers who explained it to me intelligibly.
Guess flat-earthers ain’t buying the daily flight paths, eh?
(I spent a few years underwater, so we may have taken longer paths to avoid mountains*, but I was just pushing, not steering. ; - )
*Just kidding – when making ocean transits, we didn’t travel too deep.
If the original question has been settled, would chucking out a gratuitous 3D geometry problem regarding spheres count as a tangent?
If not here It is: four spheres each with radius =1 are placed on a level surface so that segments connecting the centers of each sphere describe a square. Now imagine four more spheres of the same size are introduced so that each one sits atop one one of the original spheres. The segments connecting each the centers of each of the new spheres likewise describes a square. In fact if vertical segments connecting each new sphere to the one directly below it, all those segments taken together describe a cube.
The question is: what is the volume within that cube but not included in any of the spheres?
The volume of the cube minus the volume of one sphere, if I’m visualizing it correctly on a quick read-through. (I’m not visualizing any tangents though. ; - )
Here is one my stepson encountered in middle school, but no spheres.
A cake is is baked in the shape of a cube and frosted on the top and each vertical side (but not the bottom). The cake is to be shared equally between five people with each receiving an fifth of the cake and frosting. Describe how the cuts can be made with a chef’s knife to create five intact pieces to satisfy the requirements.
*No clever work arounds allowed. So for example no blender can be used and neither may the frosting be scraped off and distributed separately.
Dale is right. 2^3 - 4*pi/3.
It took longer than it should have, my geezerish brain being less sharp than in its youth, but the solution is fairly simple as of course you know.
It’s based on 5 x 4 = 20. Looking from above, mark each edge into 5 segments for a total of 20, and then count 4 across the near edge and cut to the middle. Then count four more, one on the near edge and three on the right edge… and cut to the middle. Similarly for the three remaining pieces, the black lines indicating the cuts. So each piece has four segment widths of frosting on the vertical sides of the cake and are thus equal there. It wasn’t intuitive to me (it probably should have been) that the three pieces that included both sides of a corner were the same area on the top surface of the cake as the two which only had one straight outside edge – hence the red lines to calculate the sum of the areas of the two triangles constituting those corner pieces. So there are five pieces fulfilling the requirements of the puzzle. Ta da and woo hoo. 

My solution is to cut the cake so each of the 5 pieces has one of the 5 sides with icing on it. You cut into the edges on the side of the cake at 45 degree angles, and cut into the top edges aiming for a central point 2/5 of the way from the bottom of the cake. That way the top piece is a pyramid with a height of 3/5 of a side, and thus has a volume (1/3 aa)(3/5 a) = 1/5 aaa – one fifth of the volume of the whole cube. The other four pieces all having the same shape as each other must have a volume of 1/4 of the remaining volume 4/5 a^3 which is therefore 1/5 a^3 each. Thus all 5 pieces have the same volume and the same amount of icing.
This solution is not so practical in practice. LOL So Dale’s solution is the one you actually want to use.
Well I can see the answer and if I were smart enough, armed with two equilateral triangles I should be able to reverse engineer the question…
Yes. SPOILER ALERT Sorry but I can’t seem to make the blur function work from my phone
.
.
.
.
.
.
.
Or more generally just divide the perimeter of the cake into five equal lengths starting anywhere you like. Then make cuts from them to the center and you’ll have a solution. The seemingly worrisome corners don’t truly matter. Dale’s visual aid helps us see that the perimeter of the cake as seen from above makes up the base of what are triangular sections regardless of where you make the cuts, and of course the height of each triangle is the perpendicular distance from the center of the cake to any of the cake’s four vertical sides which will always be constant.
My stepson’s teacher prefaced the problem by saying she’d been given it to work on at a conference she is attending but most had not yet finished it. She gave it to his class to work on for a bit at the start of class before launching in on a planned lesson. He realized why this general solution would work and wrote it down. When he handed it to her on the way out her reaction was it couldn’t be so simple surely. But of course she realized it was.
@Dale looks like we are both strong visual learners/thinkers. Does that mean you harbor a godless streak or is it I who harbor a soft spot for God?
Edited to add that I think this is a problem that becomes more complex given the amount of math you know. A strong intuitive grasp of some pretty basic math gets the job done whereas a mindset to analyze the problem by way of some more complex approaches obscures the simpler solution.
Dale, your solution seems elegant enough - but either I’m missing something, or some people are getting more cake (and frosting) than others.
The two larger triangles have an area of: (1/2) x 8 x 5 = 20 each, right?
The opposite corner piece has a 4x4 square in it (= 16), and then two (5 x 1 / 2) triangles yeilding a total top area of 21 for that piece.
[my bad! I should have stuck with your handy triangles, as my attempt above ends up double counting one of the little squares! Or another (correct) way would be to take the full 5x5 and subtract out the two (1/2)x1x5 triangles giving the desired 20. …Very nice!]
And I don’t plan to even try to evaluate @mitchellmckain 's solution. If his is right, I’ll take his word for it, and would happily eat any of your pieces of cake in any case! 
I lost sleep (more) sleep over this!
Mitchell’s actually made sense to me. I was thinking about how to exploit the 5 smooth sides of frosting, and even how to cut it with my long, thin, filet knife.
I haven’t had time to pull out graph paper, a compass, protractor and pencil to work through Dale’s, but it seems like someone is getting jipped since the cake is square. It’s been so long since I did this kind of puzzle…
Later. My tools are handy.
@merv, I have to fiddle on paper to see what your “my bad!” is talking about.
I am not. Hint? Drawing? Something?
Still dunno what the question is! Used to be an algebraist!
Terry’s was first:
After contemplating spheres and cubes a bit, MarkD veered off into cake:
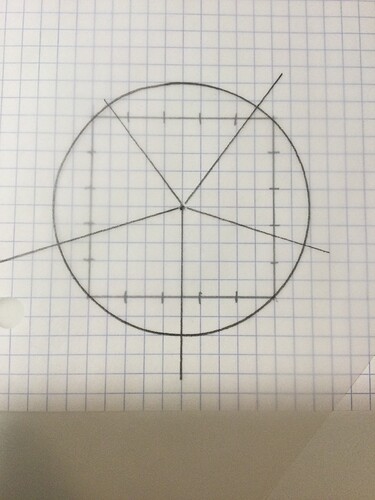
Figures 1 and 2
The first two drawings are my “evidence of inequity” in cutting the square cake in 5ths. Sorry @Dale . I cheated and used a tracing paper overlay, so I didn’t need to redraw everything. Sorry for the blur.
Just counting squares between the perimeters of the circle and square, it really seems like the person who gets that center top piece is losing out.
Top center, I count about 12 little squares missing from the cake.
L and R sides, next sections down, I count about 9 little squares missing.
L and R sides, bottom sections, I count about 7.5 little squares missing.
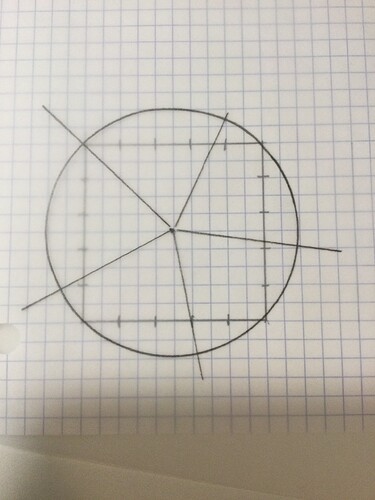
With the next arrangement of pieces, the numbers are a little different.
Top Left high and low pieces are missing about 11 little squares.
Top right and bottom left are missing about 9+ little squares.
Bottom right is missing about 8.
In the end, you know some kid is going to cry.
Figure 3
This is what I understand @mitchellmckain to have described. The orange lines are the interior cuts, and then the top and side edges are cuts.
My problem is not that I do not believe or trust Dale’s answer, but that I almost get dizzy trying “to see” the answer. Same goes for "the cake division problem, and I still have a question about my original two equilateral triangles.
But I’m right in the middle of “visualizing” the cake problem, so I’m going to finish working on that before addressing the other two problems.