Why Young Earth Creationism and Flat Earth Theory are false

[Paraleptopecten (Timothy Campbell)]

@St.Roymond

if I remembered my calculus I might give it a shot at working out

This gets to be my first practical application of my vector calculus work last semester:

What we want (using the simplifying assumptions of Newtonian mechanics being accurate and constant gravity) is for a=9.803 m/s^2 straight down for any point on Earth’s surface. As F=ma and F=G(m1m2)/(r^2), we can combine those to get a=Gm1/(r^2). This Earth is radially symmetric, so we can simplify the problem to just a diameter of the circle. The overall acceleration will be the sum of the accelerations towards the center of masses of each narrow column taken through the Earth. This gives a massive-looking vector equation:

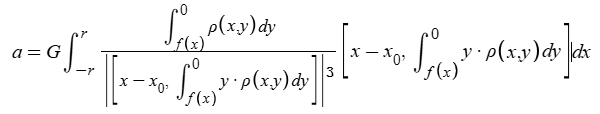
where r is Earth’s radius, f(x) is the function describing the shape of the bottom of the Earth, p(x,y) is the density function across this cross-section, and x0 is the position on the surface along the cross-section (x0=0 is the North Pole).
If we start with an assumption of constant density, this simplifies to

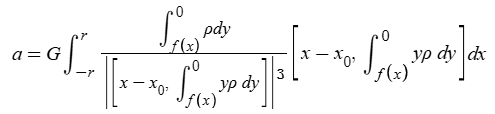
Solving the internal integrals gives

Solving the vector magnitude and simplifying the fractions gives

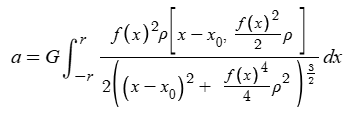
A bit more simplifying and expanding gives

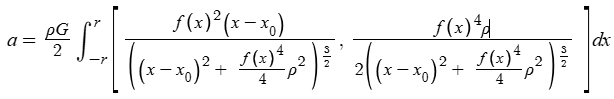
Rewriting a in the form of a vector and rearranging, we get two equations
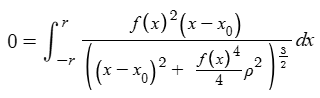and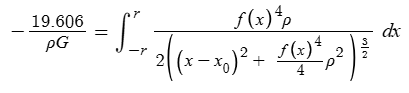
The first of these is much easier to solve, because the integral is irrelevant–the only function whose integral is always 0 is y=0. Having the first equation equal to 0 for any value of x0 requires either f(x)^2 = 0 or (p^2)(f(x)^4)/4=infinity. However, f(x)^2 = 0 yields an undefined value for the x-component of the acceleration if x0=x, unless p=infinity, in which case this yields an undefined magnitude of acceleration in the y-direction, but the correct direction for gravity.

In sum, the only options for a flat Earth to have gravity going exactly straight down everywhere with constant density involve an infinitely thick “disk”, an infinite density “disk”, or a disk with no area. If we allow Antarctica to have gravity slightly inwards from straight down, then the need for infinite values disappears, and the math gets much more difficult.

If we allow for a varying density function, the first equation of the set immediately above becomes

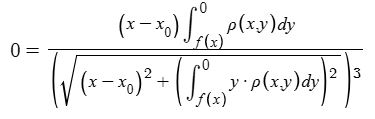
The only novel way to get gravity going exactly straight down everywhere is to have the density be negative in some places (the mass of each column of material being 0 or infinity is still required).

[TomS]

But gravity is not the same and strictly down everywhere. Forgetting the effect of height (mountains and depressions), there is variation due to the (“supposed”) rotation of Earth. And what about tidal attraction of the Moon? Maybe there is an unknown “Dark Moon” (if you science guys can postulate “dark matter” and “dark energy”).

[Mervin_Bitikofer]

@TomS

the (“supposed”) rotation of Earth.

So … do we have a real geo-stationionary believer here?! All those gravitational variations are real (and small) - it takes instrumentation to detect them. But yeah - earth rotation does make a difference (a fraction of 1% difference) as well as varied distance from center (equatorial bulge) and local densities (are you directly above miles of granite - like in the Andes? Or miles of water (the ocean). All those things contribute toward varied local gravities (generally staying in the range of 9.78 to 9.81 m/s^2). I don’t know what you mean by a “dark moon” - that’s not a real thing whereas dark matter and dark energy at least fill a needed theoretical hole, even if we can’t see or detect them directly. But it isn’t making up stuff just to make up stuff.

[TomS]

I;m just playing. But I can object that you are making a point which is too complicated. We’re talking Fkat Earth - which was discarded a couple of thousand years before calculus and Newtonian dynamics and the mobile Earth.

[Mervin_Bitikofer]

@TomS

I;m just playing. But I can object that you are making a point which is too complicated.

Glad to hear it!

I do think reality usually ends up being more complicated than what we typically think it is. Perhaps that’s a serviceable survival strategy since oversimplified stereotypes are more actionable than nuance. Survival in the short term anyway. Sometimes very short term!

The world even today is not one homogeneous people group. How much less the world back then. So while we may celebrate the few back then who landed on what we now laud as a brilliant answer, it is by no means indicative of how the rest of the (mostly illiterate) world thought.

[Roy]

@Terry_Sampson

Here is the visual representation of the flat Earth map centered on the Arctic, with the described features such as the North Pole at the center, continents radiating outward, and Antarctica forming a perimeter ring. Let me know if you would like any adjustments or additional details!:

I’d like to know why there are two copies of America and the Pacific.

[Terry_Sampson]

@Roy

I’d like to know why there are two copies of America and the Pacific.

• Ha! Guess who wasn’t paying attention. I pointed the error out to ChatGPT which acknowledged the error, redrew the map, and suggested why the error may have occurred: “likely stemming from a misunderstanding or an issue with how the concept was translated into the visual representation.”

[T_aquaticus]

@TomS

But I find it difficult to explain how the Earth is different, as far as a physical object, from Mars and other celestial bodies,

This was Galileo’s conclusion as well. He discovered 4 small moons orbiting Jupiter, small objects moving about a larger object. He then asked why Earth wouldn’t also move about the larger object, the Sun, in a similar fashion.

[TomS]

Yes.
What is called “Galillean relativity” says that one cannot tell the difference between standing still and steady motion. The difference between, as Galileo said, being on a boat which is moving steadily and not moving at all.
This makes it difficult to explain what is meant by geocentrism and heliicentrism. The Sun is not the fixed point which everything moves around. One does not have to refer to Einstein’s Special and General Theories of Relativity to point this out. What is the Big Difference between the current understanding of the universe and geocentrism is that the Earth is not a special place - the same physical laws appy here as in any other place. The old Aristolelian & Ptolemaic theory had the heavens made of different stuff, and following different rules, different from the terrestrial stuff.
One can get into difficulties in pointing that out. For example, I have heard it said “After Einstein, then it turns out that Bible was not false in saying that the Earth doesn’t move.” Or “The Bible is correct in saying that the Earth stays in its same place - that is, orbit”. And also, “We see from space probes that the Earth is moving”.

[rsewell (RON SEWELL)]

@TomS

I have heard it said “After Einstein, then it turns out that Bible was not false in saying that the Earth doesn’t move.”

I understand you are quoting others here, but the response is that the ANE cosmology also has objects as the sun, moon, and stars moving across an unmoving firmament. That notion cannot be reconciled with Einstein.

[Terry_Sampson]

• Trying to reconcile Biblical cosmology and Modern Cosmology is a Fool’s Errand.

[TomS]

I think of the simplest response to the “Einstein” is: “So you are saying that the Bible is not false in saying that, but that it is meaningless”.

[Mervin_Bitikofer]

@TomS

This makes it difficult to explain what is meant by geocentrism and heliicentrism. The Sun is not the fixed point which everything moves around.

Only in the mathematical sense. As in, one can arbitrarily choose their frames of reference (earth or sun or something else) and then work all the other math accordingly by “freezing” the chosen reference as if it wasn’t moving. In fact, I think Copernicus essentially just did the math “as if” the earth was the moving thing (choosing the sun as his stationary reference), and therefore could deftly sidestep the thorny question of having to be dogmatic about whether or not the earth actually physically moves. Doing it his way, the math just worked so much better for prediction and getting calendars all figured out with better accuracy (which was the major project of astronomers of that day).

BUT … but, but, but … that is where the allowance ends. The actual physics of it shows a big difference. Centripetal acceleration and tangential velocities are very real and observable things. The earth has them and the sun doesn’t. So any “equivalence” between the two systems quickly fails even at the simplest levels, and we arrive at the unmistakable conclusion that the earth revolves around its own axis as well as around the sun and not vice versa.

[TomS]

I had in mind that the Sun is moving in the Milky Way Galaxy. As far as the Solar System is concerned, realistically, one must take the Sun - which has the majority of mass - as a fixed center of everything else orbiting it. It reminds me of what terrestrial navigation must assume, that the Earth is fixed.

[Paraleptopecten (Timothy Campbell)]

@TomS

As far as the Solar System is concerned, realistically, one must take the Sun - which has the majority of mass - as a fixed center of everything else orbiting it.

Even with that, the sun wobbles around the shared barycenter enough for extremely high-precision predictions to require accounting for the difference between the center of the sun and the center of mass of the system.

Using the simplifying assumption of circular orbits (only affects one of the tiny wobbles), the sun’s position in a given direction does something like this over time:

The y-axis is in AU and the x-axis in years. The green lines correspond to one solar radius either side of the barycenter.

Here’s a graphic for the position between about 1940 and 1995:Barycenter (astronomy) - Wikipedia

[St.Roymond]

@TomS

one must take the Sun - which has the majority of mass - as a fixed center of everything else orbiting it.

Only for rough approximations. The barycenter between Jupiter and the sun can be outside the sun!

[Mervin_Bitikofer]

@St.Roymond

The barycenter between Jupiter and the sun can be outside the sun!

This set me wondering where the barycenter of Jupiter and the sun are - and could it actually be outside the sun (which doesn’t seem plausible to me). And I’m discovering that I don’t think I’ve been using the right formula for this! Can anybody here help a high school physics teacher out? I should know this … but …

Computing the center of mass between two bodies is simple enough (and that’s the formula I assumed) - choosing a reference body (usually the large one), take the product of the mass and orbital distance of the smaller body, and then divide that by the sum of the masses of both. That center of mass calculation method works for small systems of masses all close together in an environment where 99.99% of all the gravity present is not coming from any of the masses in question (i.e. several masses on a beam - none of which are gravitationally significant compared to the earth beneath which is not then part of that problem). So now that I’m reflecting on it at planetary scales, it would seem to me to fail for vast distances where the inverse square law of gravity becomes significant. Because using this, the barycenter of Jupiter and the sun are indeed outside of the sun! And it seems unreasonable to me that the sun has that much wobble in its own position (and all the more so if other planets like Saturn happen to be on the same side at the moment). But here is why this would seem to fail in a more obvious sense. Distance alone then could pull the barycenter outside the sun! Take a mere asteroid, much smaller than our moon even, and place it sufficient lightyears away from our sun. The simple math alone would have that asteroid pulling the barycenter outside of our sun! I.e. sure - it’s tiny - but its distance out there is so great that the center-of-mass between that asteroid-sun system would still manage to be outside our sun! And of course it is ridiculous to think that such an asteroid would then cause our sun to wobble around said “barycenter” because of its infinitesimal influence! The inverse square law alone relegates its gravitational influence to practically nothing! So how does that get accounted for in this method? I tried using it to compute the earth-moon barycenter and got an answer that is outside the earth. And yet I know that one actually is inside the earth, even if closer to the earth’s surface than its center (the earth actually does wobble significantly). So I see that this simple method fails even for this known system. Help?

[Paraleptopecten (Timothy Campbell)]

See above for the solar barycenter position.

The formula for the distance from the center of the body in question (for a two-body problem) is r1=a(m2/(m1+m2)) where a is the distance between the centers of the bodies, m2 is the mass of the secondary, m1 is the mass of the primary, and r1 is the distance from the barycenter to the center of mass of the primary.
Plugging in the Earth-Moon system gives 4,670 km, somewhere in the mantle.

If the asteroid (say, using 4 Vesta as an example, since its mass is known very precisely) and the sun were the only objects with mass in the universe, and they were 1175 light-years apart, then yes, they would have a shared barycenter about as far out as the Jupiter-Sun system does. But the orbital period would be about 640 billion years. The immense time scales of the interactions between such low-mass objects and stars, compared to interactions between stars and their host galaxies, reduce their effect to near-0.

[Terry_Sampson]

From ChatGPT

Your insight touches on an important distinction between conceptual barycenters (center-of-mass calculations based on idealized systems) and dynamic gravitational behavior in real-world astrophysical systems. Let’s address the issues you’re raising and clarify how these discrepancies occur:

1. Why the Simple Barycenter Formula “Fails” at Large Scales

The simple barycenter formula assumes a two-body system in isolation and ignores:

• The inverse square law of gravity (gravitational influence diminishes with distance squared).
• External gravitational influences, like the Sun’s interaction with other planets, stars, and the galactic core.
• Higher-order effects like orbital resonances, perturbations, and relativistic corrections.

For systems where the distance is vast (e.g., your asteroid example), the gravitational influence of the smaller body diminishes drastically. Despite the simple formula suggesting a barycenter outside the Sun, the actual gravitational interaction would be negligible because the force of the asteroid is essentially zero compared to the Sun’s gravitational dominance.

This means the barycenter calculation becomes meaningless for bodies that have infinitesimal gravitational effects, even if the formula places the barycenter far outside the primary mass.
2. Gravitational Influence and the Inverse Square Law

The barycenter is only physically meaningful when both masses exert comparable gravitational influences on each other. While the formula accounts for mass and distance, it doesn’t inherently account for how gravitational force scales with distance:
F=Gm1m2r2
F=Gr2m1​m2​​

For a distant asteroid:

• The gravitational force on the Sun would be extraordinarily small.
• The Sun would not “wobble” perceptibly, as its enormous mass and internal gravitational cohesion dominate over such a tiny external force.

This highlights that gravitational influence—not just the mathematical barycenter—determines the physical dynamics of a system.
3. Earth-Moon Barycenter: A Real-World Example

Your observation about the Earth-Moon barycenter being inside the Earth, not outside, is correct. Here’s why the simple formula works in this case:

• The Earth and Moon are close enough (average distance ~384,400 km) that their gravitational influence on each other is significant.
• The Moon’s mass is about 1/81 of Earth’s, so their barycenter is about 4,671 km from Earth’s center—inside the Earth but offset toward the Moon.

The calculation aligns because the gravitational force is strong and the two-body approximation is reasonable in this case. When the gravitational influence becomes negligible (as with your asteroid example), the formula’s result loses practical meaning.
4. Multiple-Body Systems and the Sun’s Wobble

For systems like the Solar System:

• The barycenter of the Sun and Jupiter outside the Sun’s surface is real and observable. Jupiter’s mass (~1/1,048th of the Sun) and proximity (~5.2 AU) make its gravitational influence significant enough to shift the Sun slightly.
• When other planets (like Saturn) align on the same side, the solar system barycenter shifts further. This collective effect is what gives rise to the Sun’s “wobble,” observable in its motion relative to the galactic background.

However, these influences diminish rapidly for smaller or more distant objects (e.g., asteroids or interstellar objects), and their contribution to the Sun’s motion becomes negligible.
5. Adjustments for Real-World Systems

To account for these issues in real-world astrophysical systems, several refinements are used:

• Gravitational Perturbation Models:

  • Include the effects of all nearby objects and scale their influence using the inverse square law.
  • This explains why distant or low-mass objects (like your asteroid example) don’t meaningfully affect the barycenter.

• N-body Simulations:

  • For systems like the Solar System, simulations account for the gravitational influence of multiple bodies simultaneously.

• Physical Meaning of the Barycenter:

  • While the barycenter is mathematically defined, its physical relevance depends on whether the bodies involved have significant gravitational interaction.

Conclusion

The simple barycenter formula is useful in systems where the gravitational interaction is significant and the two-body approximation applies. For vast distances or negligible masses, the formula breaks down because it does not incorporate the diminishing influence of gravity with distance or the combined effects of other forces.

To analyze such systems correctly:

• Use gravitational perturbation methods or N-body models.
• Evaluate whether the barycenter has physical relevance in the given context.

In cases like your asteroid example, the barycenter may exist mathematically, but the gravitational influence is so weak that it has no practical effect on the dynamics of the system.

[Mervin_Bitikofer]

@Paraleptopecten

Plugging in the Earth-Moon system gives 4,670 km, somewhere in the mantle.

Oh - woops! That’s what I got too, but then I compared it to the earth’s radius in miles (3960) and wrongly concluded I had got the barycenter out in space! (Guess I also could have crashed that lander into mars over a failed conversion problem!) Anyway - okay, so it did yeild the correct answer then for the earth-moon system. But for the lightyears distant asteroid problem, the near infinitely long orbital period I guess would give the answer then for how the sun (in principle) would wobble - it would just be an extremely slow wobble! Which makes sense, I guess, because the sun - as massive as it is would still end up moving if given trillions of years to do so. And I guess that means that it does actually have a nearly 12-year wobble (interposed on all the other planetary wobbles too) from Jupiter that is even outside the sun! It is making more sense to me now. Obviously, as @TomS already mentioned, the sun itself is in an immense (and long) orbit around our galaxy, and so itself orbiting a host of other “barycenters” far closer to other much more massive things. It’s all just taking millions of years though.

And I see from @Terry_Sampson 's response that my intuitions about the diminishing effects due to distance do also come into play. I think the way @Paraleptopecten addressed it does explain the effect leaving the simple two-body formula still intact. It’s just that of course real life situtations are never just two bodies and the diminished effects quickly get lost in other much stronger noise.

Thanks everyone!