Thermodynamics question

[pevaquark (Matthew Pevarnik)]

@Dale

It appears that it will have been fairly recently, in a cosmological perspective.

If you consider objects at increasing distances from the Earth, to a decent first approximation, they follow Hubble’s law:

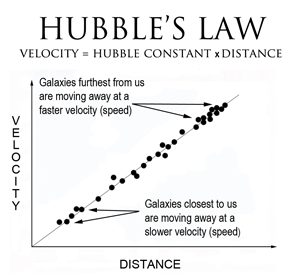
The equation for this is:
v=H_0d

Where v is the recessional velocity, H_0 is the Hubble constant and d is the distance of the astronomical object. The Hubble constant has a value somewhere around 70 (km/s)/Mpc. You will note that this has units of distance/time divided by distance (or inverse time). It is a slightly odd way to write the constant, but it can be quickly used to calculate how fast an object at a certain distance is receding from the Earth due to the Universe’s expansion.

Side note: to calculate this more precisely, you should use the Friedmann equation, which describes how the Hubble expansion changes as a function of the density of stuff inside the universe, but that is beyond the scope of my post here.

Back to our estimate, we want to know at what distance does:
H_0d>c

where c is the speed of light. Doing a little aligning of units gets you d>4.3 GPc which is 4.3 gigaparsecs or about 14 billion light years which is what you found in the article posted above. Put another way, an object that is presently at or more than 14 billion light years away is presently receding away from us faster than the speed of light (assuming a constant Hubble expansion rate). This cutoff point wouldn’t necessarily change for most of the universe’s history. However, with a now accelerating expansion (unless dark energy is more interesting than a cosmological constant), this number will gradually start decreasing. In principle, the most distant galaxies that we can presently observe (now further thanks to JWT) will gradually become more and more redshifted until they disappear from our sight entirely.

None of this answers your questions per se about when did cosmic expansion exceed the speed of light, but here is a short video that talks about some of these things:

Misconceptions About the Universe

To answer your question can also be done I suppose to a first (very simple) approximation by asking this question, now that we found the magic distance of about 14 billion light-years where we then say how long would it take with an object’s speed continually increasing as it moved away from us (or the location where Earth would someday be) to reach this magic cutoff point of 14 billion light years away. Maybe we could write something like this:
dx(t)/dt=H_0x(t)

The main idea here is that the velocity is turned into the first time derivative of distance from Earth, and the distance from Earth changes as a function of time.

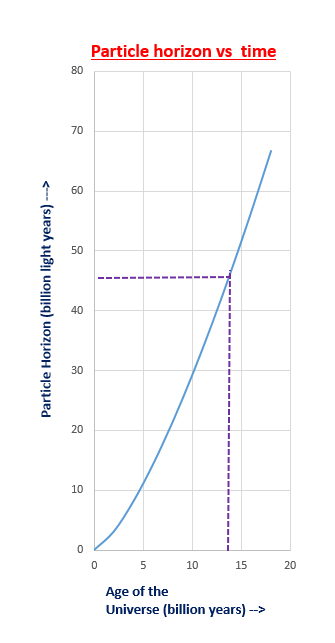
Edit: usually this is done via the scale factor of the universe, but a plot of this distance (also called the Particle Horizon) is shown here:

Source explaining this in more detail:

Cosmic Horizons

So @Dale, it looks like to answer your question the universe first passed the Hubble radius about 8 billion years ago.

[Klax (The only thing that matters is faith expressed in love.)]

@LorenHaarsma

Longer answer:
There are many forms of energy. Heat energy is the highest-entropy form. It’s particles and photons moving randomly in “thermal” distributions of energy. The “heat death” of the universe refers not to temperature, but to the eventual fate of all other forms of energy in the universe converting to heat energy, after which no more entropy-increasing processes (such as stars burning, or life) can occur. Since it looks right now that the universe will keep expanding forever, this will happen in our universe at a very cold tempreature.

Now regarding energy conservation and expansion:
Imagine a box full of particles elastically colliding with each other and the walls. Put that box inside an empty bigger box. If you knock a hole in one wall of the little box, the gas will eventually expand into the bigger box, increasing volume and increasing entropy of the gas without doing work, and the internal energy of the gas of particles will stay the same. If you, instead, let the walls of the little box expand to the size of the big box, the gas of particles will do work as the walls expand, and the internal energy of the gas will drop. You could tell a similar story with a box of perfect-mirror walls full of photons.

But if you have space full of photons, and space itself expands, the photons stretch in wavelength and lose energy. Does that mean that energy wasn’t conserved? Or did the energy go into the expansion of space itself somehow? We’re not sure. It seems we need a bigger, comprehensive theory that unites quantum field theory and general relativity (and, we hope, dark energy as well), and then maybe we’ll know the answer.

In my abyssal ignorance:

If space expands already intrinsically expanding universes forever then the wavelength of all photons and force particles would tend to the infinite? From 10^100 years OOM? In the Dark Era? During which no work can be done? At what wavelength do photons etc become ‘useless’? Yet…

(To your second para) There seems to be a need to factor in an energy value for the volume of space itself to maintain conservation? In the pinhole experiment you are describing black body radiation. In the moving walls scenario, if the walls expand due to an external force, then the energy is still conserved in the total expanding volume. The density decreases but the particles’ speed does not (universes have no walls). But in an ICE piston the gas particles lose energy by driving the mechanical expansion. Which seems to be an analogy for the expansion of space (but not universes).

If universes expand but space itself does not, do photons intrinsically attenuate? I was told not by a Ph.D. physicist. Newton’s first law. I infer. But, space itself is expanding, only exists where there is matter, even worse it is accelerating… so photons’ and force particles’ wavelengths must be increasingly stretching, attenuating, decaying, their frequency must be decelerating, to conserve energy?

In a perfect mirror wall box of photons there can be no expansion from within, so any externally driven expansion will not affect the photons’ frequency, just dim the light intensity. But space itself is expanding, so the photons must intrinsically redshift. Acceleratingly.

We have no warrant for breaking conservation.

Is that coherent?

Space itself has an intrinsic energy value.

And can expand faster than light when what it is transporting has a high enough density. Whence inflation.

All of which may be rationalization too far, but does make some of the ineffable strangeness of existence probably illusorily less so. It’s still stranger than God.

Hmmmm. So at what wavelength would photons become incapable of driving the expansion of spacetime (for some reason I’d either picked up or made up that it was driven by conservation breaking increasing in dark energy)? And what would happen if they did?

[pevaquark (Matthew Pevarnik)]

@Dale updated my post to answer your question more specifically. Will try to respond to a few things @Klax in next few days unless someone else beats me to it.

[Dale (evolutionary providentialist)]

Thanks for your work in that. It seems that Earth (and the humans on it) are in kind of a sweet spot for being able to observe the universe, including in time.