Ages of Patriarchs

Faith & Science Conversation
82

The attachment Chris links, “Genetic Entropy - Recorded in the Bible”, by Sanford, Pamplin, and Rupe, 2014, makes the argument that the Biblical record of decay in lifespans after the flood must be real because, quoting from the paper:
The data is coherent and internally consistent in a way that could never happen by chance.
…
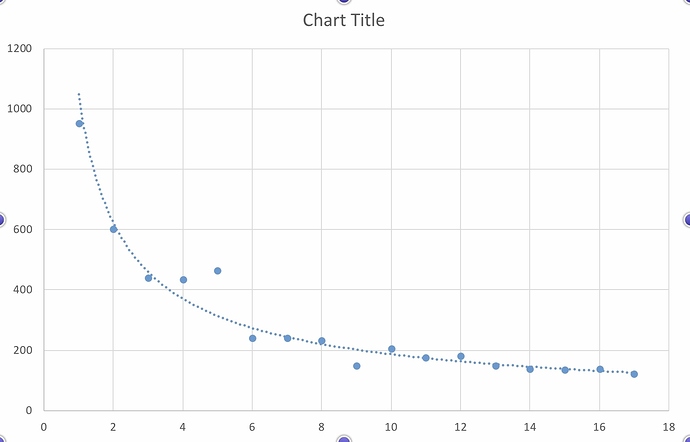
The smooth curve is shaped according to the specific formula shown (y = 1064.7x-.766).
…
The first explanation would be that the mathematical nature of the decline arose because all these data points, scattered in various books of the Old Testament, were fabricated by a sophisticated and scheming single author. That such an author would need to be a skilled mathematician.
…
The second explanation would be that the mathematical nature of the declining lifespans arose because the Biblical accounts are true, and are actually faithfully recording the historical unfolding of some fundamental natural degenerative process.

End of quotes. I think I’ve been fair in excising their essential argument, correct me if I’m wrong.

We probably are at an impasse as you suggest, but I just wanted to make clear what I meant to state in case I failed to communicate in my prior posts. True, lifespans of hundreds of years are certainly remarkable. As you observe, there is an obvious steep decline in the recorded lifespans post flood, which then levels off to more or less typical of today, depending on conditions. I am not taking a position here as to if these lifespans are real or honorary or reflecting some sort of numerology. It is surely reasonable to presume that there would be some significance to the drop off in age, but as to what it is, I have no insight. I do not know. I have no idea. I have given that little thought.

It is the assertion, however, that the data yields a mathematical curve that is, and it is in this context I use the term “remarkable”, that I repudiate. To somewhat rehash, any set of trending ordered pairs can be modeled by an exponential equation of the form given, so the lifespan data tabled here is not unique in that respect. Hence, the data is not “remarkable” in a statistical respect. The premise that the author of these lifespans would have to have been a skilled mathematician is simply invalid, because no matter what ages the author chose, so long as you have a trend, you could derive an exponential curve of the very exact same form. Only the parameters would change. I’m not even touching the concerns with data selectivity. Therefore, the conclusion that there is a hidden math, unknown to the original authors but available to us, which self-authenticates these lifespans and leaves no option but to accept them as true, is complete bunk. So my position is this and no further than this, that statistics has no bearing on the literal or literate nature of the recorded lifespans, and on that point, I believe I hold the high ground.

4 Likes
83

In addition to @rsewell’s excellent summary of the problem (or lack there of), I’d also like to point out that the author’s first explanation (quoted above) is a straw man. A weak argument, easily refuted which (even if unintentional) serves to bolster there own. Even when limiting the range to the set we are considering (the patriarchs of Genesis), there are any number of reasons why the author might use ages which are not ‘actual’. Non of which reasons, I’d point out, are scheming in any way, nor require them to be a skilled mathematician.

84

Marshall, please… You are still reading me through some kind of “creation science” lenses. I don’t know how much more clearly I can say this… It is not that I don’t want to consider the mechanism of why these very real historic ages declined… I am asking why the numbers declined, whether they represent something real, imagined, invented, symbolic, or something that came from multiple die rolls.

The “mechanism” I’m considering here could be different authors, change in genre, redacting or different sources or traditions, numerological considerations, shifts in purpose, darts against a chart, blind die rolls, etc.

And no, to recognize the edge of a cliff one doesn’t need to know the mechanism… you take measurements of elevation above sea level and find out where the elevation starts to decline. You don’t need to know if said geographic feature was cause by plates, earthquakes, erosion, man-made, or the like to notice the ground is pretty consistent for a while then starts to quickly decline.

Similarly, I don’t need to know a specific mechanism or purpose to notice the edge of the cliff, any more than I need to know the mechanism to notice a decline in general. The pattern stays relatively steady, then starts an obvious decline. And Noah is the patently obvious apex of that decline (though one alternate possibility I’d consider, see below).

I. AM. NOT. TRYING. TO. TIE. THE. PATTERN. TO. SOMETHING. REAL.

:rage:

my purpose here, again, is to explore any and every OTHER possibility BESIDES THE “REAL” HYPOTHESIS.
Tying the pattern to something real is the one hypothesis I am not interested in hearing about. I’m already generally aware of that one. I want to explore all the other alternatives. Again, from my original post…

As for where to measure the apex and/or top of the decline, there are only two possibilities I can conceive, simply thinking of the math involved.

  1. Methusaleh is the edge of the precipice / beginning of the decline, Lamech at 777 starts the decline, Noah is a high aberration, then the decline continues with Shem, etc.
  2. Lamech’s low 777 is a low aberration of the previous patterns, Noah’s 950 continues the obvious ~900+ pattern of Genesis 5, and the decline starts with Shem.

For various reasons, not least of which the chapter break between 5-11, the latter seems to me far more sensible, especially if I leave any “real” considerations out and simply consider what the author(s) is trying to accomplish… it seems more likely that Lamech was understood by the author(s) as part of the “previous” world, Noah began the “new” pattern.

But if you wanted to propose that the decline in ages, for whatever reason and authorial intent and purpose, began with Methusaleh, Noah being the aberration, I’d be completely open to your observations.

What I will not bother entertaining as anything but cherry picking, though, is your suggestion to “measure” the decline starting with Lamech as the “edge of the cliff”, or high point from which the decline started… whatever we make of Lamech’s age of 777, being smack between his immediate ancestor at 969 and immediate descendent at 950, the one thing I can confidently claim is that he is not the “high point” from which any decline should be measured.

85

“ What we know from reincarnation research is that humans live up to 30 lifetimes or about 900 years total”

Can you define the word “know”

86

image
image1380×884 85.8 KB
https://discourse.biologos.org/uploads/db1313/original/2X/6/683b2e60913d840c5c3a41f92d0fbe74497a4b55.jpeg

A lecturer of mine explained it as the Fall resulting in gradually declining lifespans. I don’t believe in this as a literal explanation, but I can see Bibical authors adopting this as an illustration of sin increasingly affecting human existence.

1 Like
87

Okay … point heeded. Maybe we can tiptoe away from that for a bit.

88

To “know” comes from knowledge, from studying a body of knowledge.

89

I’ve considered this in and of itself, and in general I think there is significant merit to that. But what gives me pause is still the strange pattern in the numbers. Why would an author trying to communicate the progressive effects of sin have essentially shown nine or so generations basically unchanged, and then only later after Noah did he decide to demonstrate a progressive decline due to the effects of the fall?

In other words, if I think of an author demonstrating, or wanting to illustrate, the cumulative or progressive corruption of humanity due to the fall, I would think that such a decline would have started with Adam, no?

Adam lived only 900+ years, which granted is a huge decline from infinity, But then the line of his descendants immediately after him showed no significant decline. Could there have been some reason that the author/authors were trying to communicate that the Deeper or more lasting or more significant effects of the fall did not start taking place until around or after the time of Noah?

90

Interesting question. Perhaps, Genesis 6:5 might hold a clue? Genesis 6:5 says,

The Lord saw how great the wickedness of the human race had become on the earth, and that every inclination of the thoughts of the human heart was only evil all the time.

It would seem that the time of Noah marks the point when total depravity becomes total. Not only in that sin effects humanity as a whole but also that also in that it taints everything they do. Even good deeds in the eyes of their peers are no longer good in the eyes of God.

Just a thought…

91

I have considered that also, and I think it’s a good thought. One would think that the consequence of the flood was the main response, however, Reduction in lifespan as a judgment could well be in view. The passage about man’s years being 120 do certainly seem to be in connection with God’s displeasure of humanity.

Seems odd to me that after the flood, you still have generations upon generations, throughout Genesis, that lived well past 120 though, even so, God does tend to delay his judgments often enough. I think of, “the day you shall eat it you shall surely die.“

One complication, is that many have interpreted the 120 years as essentially the countdown to the flood, Not a new upper limit on human lifespan. Man has 120 years left until judgment comes, not unlike Jonah’s 40 days until Nineveh is destroyed. And this is not a modern interpretation to try to solve this current difficulty, I noticed John Calvin took this approach in his commentary 400 years ago. I honestly don’t know what to make of the 120 year comment in genesis six, I could go one way or the other on that one.

Just so I followed your thought, is it that due to man’s wickedness hitting its maximum, that is when God’s judgment in decreasing lifespan began? The other difficulty with that, now that I think about it, is that in theory, all the population of the world that was so depraved would have been drowned, and it seems a bit odd that God would go forward on this Decreasing life span judgment on righteous Noah and his descendants, right after he had drowned all the people that were in fact so deprived. Thoughts?

92

Well, with increasing life spans in the last century or so, does that mean we are more righteous?
That is half tongue in cheek, but half serious in that it points out the problem with linking it to righteousness. Plus, in pre-flood days, things were so bad God wiped them all out, so why did he let them live that long in the first place? Of course, you have to have a literalist interpretation to really enter the conversation, as that is a pre-supposition of the discussion, so I am probably out of line to comment.
The environmental change with the flood lowering lifespans does not fly with me either, as no plausible mechanism is present for that sort of change. Ultimately, I think we have to accept that the account is more mythical than historical or else is clothed in miracle and outside our understanding.

2 Likes
93

I agree. It doesn’t take higher math or a geiger counter to make a series of numbers that plots a curve. Take a number and keep halving it and – presto – perfect decay curve!

In an artificial series of decreasing numbers, it’s quite reasonable for the size of the drop to depend on the scale of the number, showing bigger drops with bigger numbers and smaller drops when the numbers get smaller. No special math required, just awareness of how 900 to 800 seems about as significant a change as 90 to 80.

Yes, I know. What I’ve been trying to point out, perhaps poorly, is that setting aside reality and focusing on the way Genesis presents the numbers is the best way to make sense of them. For others (not you!) who wonder about a natural cause to the numbers, it doesn’t make sense to start with Noah (for the reasons mentioned before), and it doesn’t make sense to treat Moses and Joshua’s ages as reflective of their generation when the Bible tells us otherwise. This in itself is a strong point in favour of literary explanations, since the easiest way to explain the numbers we’re given in the context they’re placed is to set aside reality and focus on literary reasons.

If we’re looking for patterns and symbolism, it makes sense to measure the drop of a cliff from the roof of a lighthouse built at its edge. When it’s exactly 100 metres from roof to base of the cliff, it’s probably intentional. But if we’re looking for a natural mechanism for the cliff (and Daniel, I know you are not), the roof of the lighthouse is no longer a good starting point.

Back to the literary explanation. Between Noah and Abraham there’s generally a stairstep decline by hundreds, but those whose ages are given outside the genealogy (Noah, Terah, Abraham) receive significant numbers that are a bit higher (lighthouses, if you will) while still fitting the overall decline. There are two dramatic drops to indicate the importance of the two key events in these chapters: the flood and the division at Babel. While the second drop is actually bigger as a percentage than the first, it’s smaller as an absolute number. After the genealogy, the later numbers also show a decline, but rather than decreasing by hundreds like the genealogy, they decrease at a scale appropriate to the smaller numbers.

One other cool thing is that the two sharp drops create two gaps in the total ages after the flood. There’s nobody who lives in the 700–800 range, and nobody who lives in the 300–400 range. If we go back to Genesis 5, the two exceptions to its 900-ish lifespans are 365 and 777, neatly filling both gaps. So, the Genesis 5 genealogy creates a kind of flipped negative image where the two figures deviating from its pattern of uniformly high lifespans coincide with the two gaps in the Genesis 11 genealogy’s pattern of ages decreasing by hundreds.

One could speculate all sorts of reasons for such a pattern, all of which would be only guesses, but it’s one more way it looks like these numbers have been arranged and massaged over long periods of time to embed all sorts of intriguing patterns and symbolism. Like the many wordplays in Genesis, the numbers seem to be one more tool used to bolster themes already stated in the surrounding narrative.

94

Absolutely not! are you
Just jerking my chain, or am I really communicating so poorly?? Somehow, my intent in this discussion is continually being misunderstood, I’m beginning to doubt my communication skills…!

:woozy_face:

I am particularly interested in understanding what other explanations there are for the originally long, then declining, lifespans, anything but a literal Interpretation.

In other words, presuming that the ages are not literal, they must have been invented or contrived for some other reason, They must have some other significance.

Assuming that an ancient author did not simply roll dice and invent the numbers that way, and they just happened to decline (or perhaps, as he was proceeding with this method, he gradually lost more and more dice?)…

But presuming that his method was not simply random, he must have had some reason to portray those numbers as declining, even if in his own mind it represented nothing literal. I am trying to gather and explore any and all possibilities…, what could those reasons have been?

95

Is there a clue from the relatively long Reigns and lives of the Sumerian Kings?

There is also a slope down there I think.

interestingly Answers in Genesis actually has two posts about this as well, but I’ve not read them yet.

Thanks.

2 Likes
96

Sorry if I mis-communicated. I was looking at the discussion and was referring to the idea of life span relating to the the level of righteousness of man. As I reflect on these ideas however, It does solidify in my mind that the changes in ages is indicative of a transition from a more mythical narrative to a more historical account, and probably had that meaning to the original audience as well.

1 Like
97

Dear Randy,
The Sumerian Kings List brings an interesting perspective to Genesis.

To understand Genesis, you need to understand the images in Revelations: A guided tour from Jesus through the history of Heaven. There are 24 Elders around the throne of God and the dragon has 10 horns. 10 of the 24 Elders of Heaven followed Lucifer, and became part to the beast that destroyed the peace in Heaven. There are also 24 knops on the Menorah’s arms, under the seven Spirits of God, that represent these 24 elders. We have 24 ribs, 14 of which are connected directly to the sternum and 10 that are the floating or false ribs. These 10 ribs represent the ten horns of the beast.

Two of these ten fallen Elders are Adam and Eve. (Gen 2:21) The remaining eight Elders show up in the Sumarian King List as the predynastic antediluvian rulers, each ruling over Earth (and the underworld) for hundreds of centuries each. But these are not humans who lived this long, rather they are demons who ruled over unenlightened humanity before the prophets came.

98

that is especially fascinating. I’d heard of this but never bothered to look it up, I never knew there was a similar decline, I’d only heard about the extremely long ages. Thanks for this.

I glanced at that, and it almost seems in some ways for a while to reflect the same pattern as in Genesis, only exponentially greater… Antediluvian ages in the ~20,000s, then immediately after the flood, ages of ~ 1,200-600 or so.

I have no idea what these are referencing specifically, but the ages reflected in the First rulers of Uruk reflect a similar exponential decline as the kind I’m seeing in genesis 11… first 3 are still extraordinarily large (324,420,1200), then two at a huge but not ridiculously extraordinary 100 and 126, then all of a sudden numerous reigns with very realistic numbers… 30, 15, 9, 8, 36, 6, 36…

So the high beginning and then exponential decline in ancestor/early ruler ages is not unprecedented, it is paralleled here. I’d be curious, then, or further thoughts… why do either of these lists reflect a decline in ages, gradually moving from the extraordinary to the commonplace?

1 Like
99

Yes, it is sad that so many centuries went by after the composition of a Genesis where people were unable to understand it as a Revelation had not yet been written.

:cry:

100

I found this to be very interesting as well!

101

This is fascinating, yes, and is certainly I think the most plausible hypothesis I have noted. Perhaps there was the tradition of very long ages, and an author or redactor felt like adjusting the ages gradually downward to more common place numbers. However, it still baffles me why he would specifically make the precipitous drop after Noah and then move it to a more gradual decline, or, as Marshall describes it, the “steps“.

Was the author trying to say that Noah was part of the previous mythical epoch, Arphaxad, Shelah, and Eber occupied a certain distinct stage that was half-mythical or something, and Abraham’s immediate descendents occupied an epoch that was only 1/4 mythical?

I still wouldn’t do expect a relatively gradual and linear, or perhaps haphazard d Cline if this was the ancient author’s intent. Why the sudden decline. Marshall’s protestations notwithstanding, my scientific minds still sees something approximating a decay curve, and I would have to suspect this would have been intentional on the part of the author.

:man_shrugging: